Theory of Production and Cost
A firm cannot produce goods and services out of thin air. They require inputs such as land, labour (L), and capital (K). In economics, land refers to the free gifts of nature like soil, air, and water while capital refers to machines, factories and other resources. These inputs are called the
factors of production.
Production Function
The factors of production have to be combined in a particular manner to produce a certain product. Think of baking a cake which involves mixing fixed proportions of the ingredients, following a definite procedure. Indeed, baking a cake is production in economic terms. The set of all feasible combinations of factors of production and output levels produced by them is known as the production set.
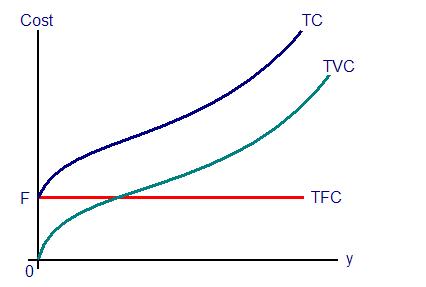
The production process can be defined over 2 periods - short run and long run. In the short run, there are some factors which cannot be varied instantly. These factors are known as fixed factors. For example, labour supply depends on the population of the country which need several years to grow. Long run refers to that duration of time during which all the factors of production are variable factors.
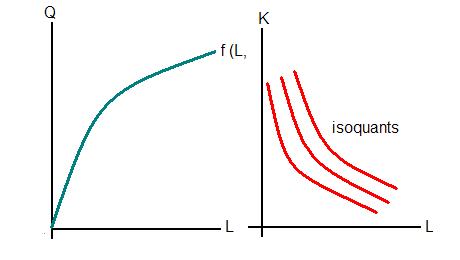
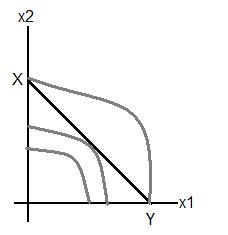
A production function expresses the maximum level of output a firm can produce using a given level of inputs. Suppose that a firm requires two inputs-capital (K) and labour (L). Its long run production function will be written as q = f (K, L). The short run production function will be q = f (L, K') where K' is the fixed input. The diagram below represents the 2 cases. Examples of production functions are the Cobb Douglas function, Leontieff technology, CES technology etc.
To go into the details of the different types of production functions avail the services provided by Transtutors.
Short Run Production Process
The second graph shows the output produced by varying one input alone, as happens in the short run. The blue line represents the total product generated by employing more and more labour, assuming labour is the variable factor in the 2 factor example.
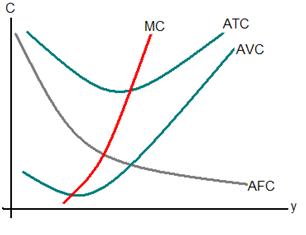
Average product (AP) is the total output divided by the amount of the input used to produce this output. Mathematically, AP for labour = f (L, K') / L.
Marginal product (MP) is the change in output produced by an additional unit of an input. Mathematically, MP for labor = ? f (L, K') / ?L. Graphically, the MP is the slope of the total product curve or the production function. It indicates the rate of change in output as the input changes.
Law of Diminishing Marginal Product
This law states that given the fixed factor of production, as the amount of the variable factor is increased, a certain stage is reached beyond which the MP declines. That is, the output produced increases but at a diminishing rate. On further increasing the variable factor, the output produced starts declining.
If you are keen to know about the properties of the average and marginal products, the empirical evidence of the above mentioned law or about the general production process in the short run, come to Transtutors. Their online tutoring and assignment help can be the answer to your problems.
Long Run Production Process
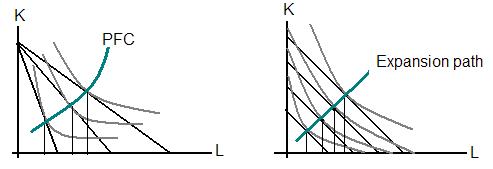
The first graph depicts the long run scenario when it is possible to vary all the inputs. The red lines represent the output produced and are called isoquants. Isoquants are the locus if the feasible combinations of inputs that produce a given amount of output.
Marginal Rate of Technical Substitution (MRTS)
The MRTS of K for L is the maximum amount of L that can be replaced by one unit of K such that the level of output produced remains unchanged. It is the slope of the isoquant.
MRTS = Δf (K, L) /ΔK which is equivalent to MP of K / MP of L.
Δf (K, L) / ΔL
Properties of isoquants:
1. Isoquants are negatively sloped because if the quantity of factor 1 used in production is decreased then the quantity of the other factor must be increased to produce the same amount of output.
2. Isoquants are convex to the origin. This is because of the principle of diminishing MRTS which states that as the more and more L is substituted by K, the MRTS decreases. Note that this principle is an extension of the law of diminishing MP.
3. Higher isoquants indicate greater output yield.
4. Isoquants do not intersect.
Elasticity of Substitution
This is measures the relative change in the input ratios in response to the change in the MRTS. It is calculated by dividing the percentage change in L/K by the percentage change in the MRTS of K for L.
Returns to Scale
The law of diminishing marginal product applies in the short run when labour is the only variable input. In the long run, a firm can change the scale of production by varying all its input. How does the output change in that case? At the beginning of the period, there occurs increasing returns to scale followed by constant returns to scale. If the inputs are increased further then there is decreasing returns observed also.
Increasing returns to scale (IRS) - This implies that if all the inputs of the firm are increased λ times then more than λ times output will be produced. Mathematically, f(λK, λL) > λf(K, L). The IRS can used in defence of mergers because one logical extension of this condition is that two identical small firms would produce more output if they were to combine their resources and become one large firm.



 CAclubindia
CAclubindia